RRI関数で貯蓄型保険の化けの皮を剥がす：満期受取額から年利（金利）を計算する方法

RRI関数とはエクセル（Googleスプレッドシート含む）の関数の一つです。

関数仕様は後述しますが、非常にシンプルな関数です。その割にはこれを知っていればセールストークに引っかかる人がどれだけ救われたかと思うくらい、マネーリテラシーを語る上では超重要な関数じゃないかと最近思っています。

一つ例を挙げます。

上のウマウマ部分を読んで、「全然ウマウマじゃねーよ！」と思う方はこの先を読まなくてもいいかと思いますが、自分は最初この話を聞いて、ウマウマだと思ってしまいました。

これは、年利と複利の考え方が実例に置き換えて考えられていないことと、利率の相場感を知らないことで起こる悲劇なのかなと思います。

上の例で挙げている8%は言ってしまえば「17年利率」みたいな感じで、17年後何%増えているかです。

しかし、世の中の投資商品の利益や銀行の利息は「年利率」（年利：もっと正確に例えて言うと「1年利率」）で語られていますよね。

つまり、フェアに利率を比較するためには、「17年利率」を「年利率」（1年利率）に変換する計算が必要になります。それがRRI関数になります。

RRI関数の関数仕様は下記になります。

今回の例で言うと、17年利率から1年利率を求めるので下記になります。

IRR（17, 5700576, 6156800）= 年利約0.45%

年利0.45%ってどれくらいなんですかね。以前記事に書いた楽天銀行の普通預金は0.1%です。他の銀行を調べると、定期預金によっては0.2%近いものもあったりします。

一方で長期で固いインデックス投資の平均年利率は、20年スパンで米国株（S&P500)で8%[高っ！！]、国内（日経平均）で0.8%[低っ！！]と言われています。（注意：参照元が少し古い記事です）

つまり、確かに定期預金よりは年利がいいけど、インデックス投資に比べるとはるかに劣っていると言うことがわかります。

ここまで分かって初めて同じ土俵に立てます。インデックス投資は元本保証がなかったり、生命保険は資金拘束に加えて保険会社の倒産リスクがあったりして、最終的にどこにお金を預けるかは本人の判断に委ねることになります。

安易に増えた分だけ見て「結構増えてんじゃん、素晴らしい保険だ」と思う前に、数字のトリックに惑わされているかどうかを確認する必要があります。

ちなみに、ここまでの説明はかなり要点を絞って説明しています。「複利」とは何か？、RRI関数は月利も出せたりする補足などは、いつか説明できたら説明します・・・。

ここから先は、おまけです。

先ほどの1年利率の計算結果を検算してみました。

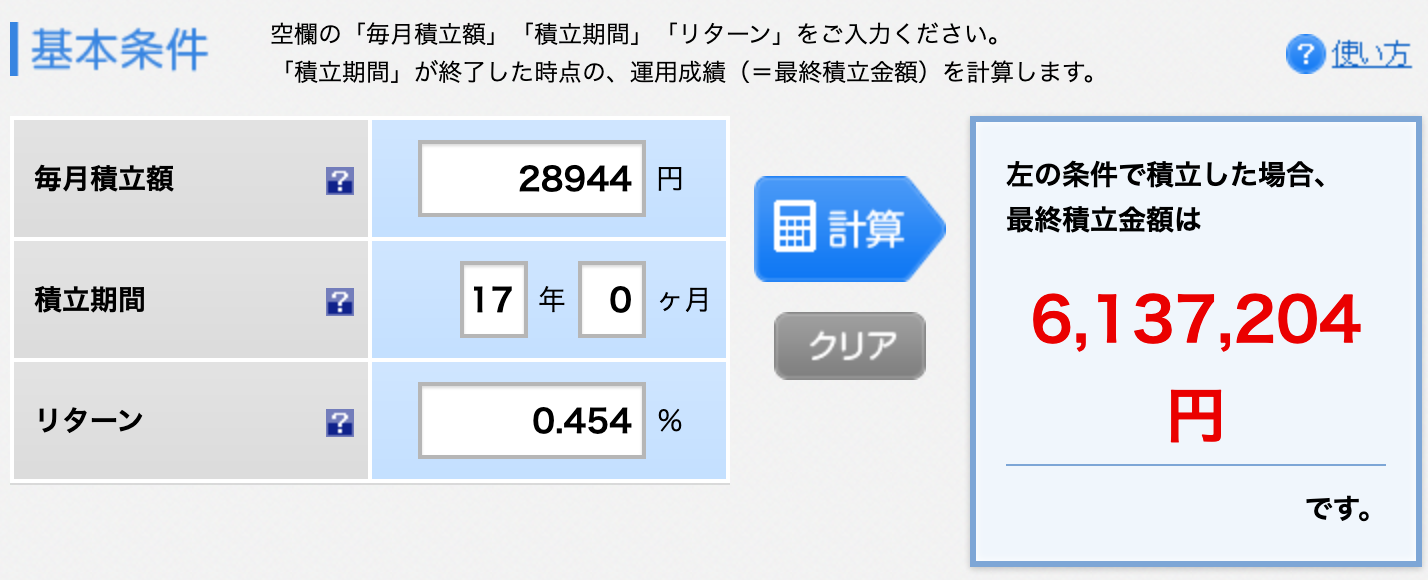
つみたて投資のトータルリターンを計算する楽天証券の積立かんたんシミュレーションで年利率0.45%を毎月28,944円積み立てると下記になります。

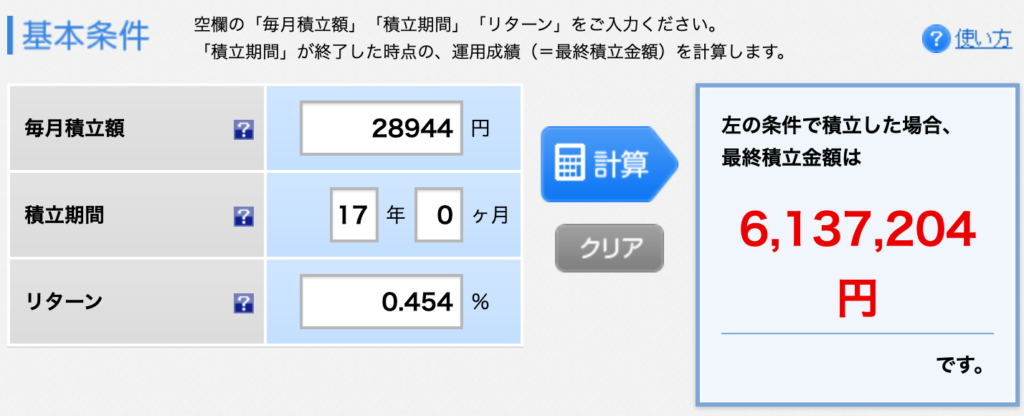
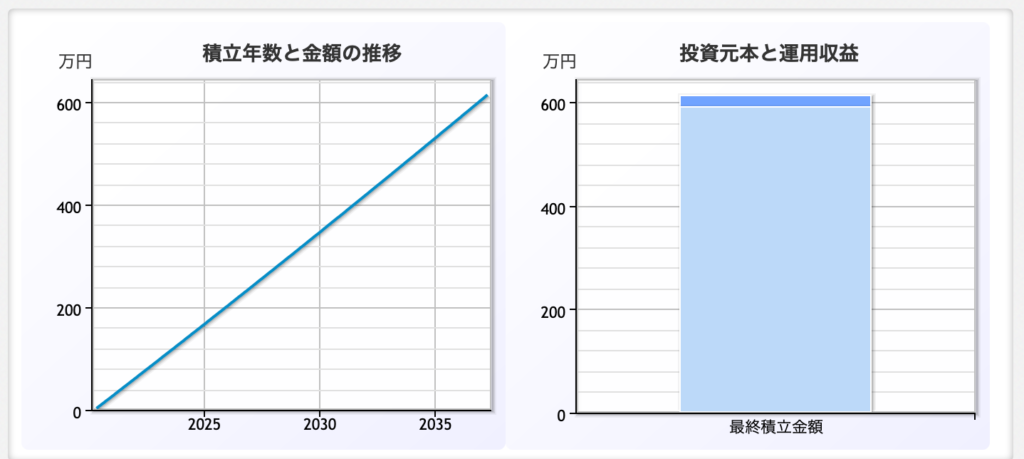
RRI関数の結果を小数点以下切り上げたりしたので、ぴったり一致はしませんが、ほぼ同じですね。

マックス

しかし、全然増えてないな、これ。

マックス

TwitterInstagram

40代に入り、急速におっさん化している日々の成長？を記録しています。主にお金、サウナ、自己投資について、経験や気づいたことがお役に立てれば幸いです。 アメブロ別館（こちらは雑記メインです）