「標準偏差とは何か?」を数式を使わずに説明してみる:知ることで人生の勝率が上がっちゃう!
標準偏差は重要です!
というのを昔の受験の参考書に書いてありまして、そこから標準偏差に興味を持ちました。
アラフォーとなり、これまでいろいろな場面で標準偏差が出てきていたので、今回は標準偏差でどんなことが分かるのかを実際のデータを含めて説明したいと思います。
ズバリ、標準偏差の重要性は知ることで人生の勝率が上がることにあります!

通常は標準偏差の定義式から始まるのですが、この記事ではなるべくスラスラ読めるように数式を登場させずに説明します。
その代わり、実際のデータを紹介して具体的(実践的)な形にしてみました。
標準偏差がどんなことに役立つのか知りたい人、特に以下の人には読んで欲しいです
- 受験生の方
- 投資初心者の方
- ソフトウエア開発の方
- その他、不確実な情報を扱う方全般
標準偏差・・・の前に、不確実なものを扱う場合に使われる正規分布について
標準偏差を理解する上で登場するのが正規分布です。
正規分布は世の中のあらゆる確実ではない事象(この場合、確実とは「絶対、何があってもこれしかありえない」という意味)を扱う場合に使われます。
確実ではない・・・つまり不確実な事象とは具体的に何でしょうか?
- サイコロを振った時の出た目
- テストの点数
- 身長や体重、年収
- 株価や配当金
- 見積もりと実績の誤差
- (挙げればキリがありません・・・)

上記でも膨大な要素を計算して「必ずこの値になる」と言えれば不確実ではないのですが、現実的には無理なためここでは不確実な事象と言います。
これらの事象がもし、不確実ではなく確実な事象であれば、同じ条件で何回実施しても結果が同じになるはずです。
つまり、ある値が何回発生するかのグラフ(分布図)は以下になるはずです。
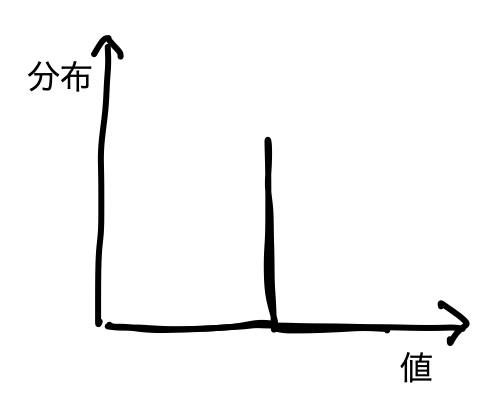
特定の値が出続けて、他の値は一切でません。
すごく分かりやすいです。シンプルです。
しかし、不確実である以上は同じ結果にはならず、異なる結果が発生することがあります。
そのブレ(誤差といってもいいかもしれません)は一般的に実施すればするほど、正規分布に近づくとされています。
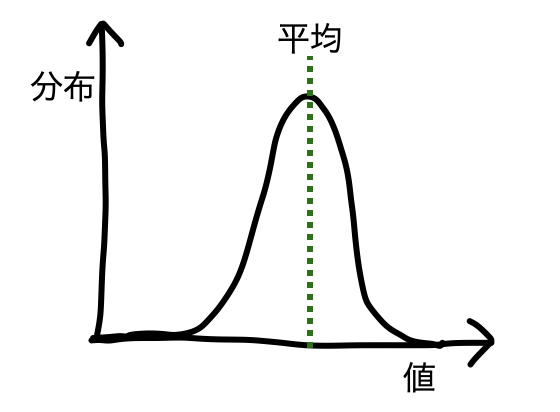

正規分布のイメージとして、
あまりに誤差が大きなケースって発生しにくく、誤差があってもほとんどの場合は小さい誤差でしょという感覚でOKです。
この形を決定づける重要な要素が標準偏差なのです。
標準偏差とは何か?
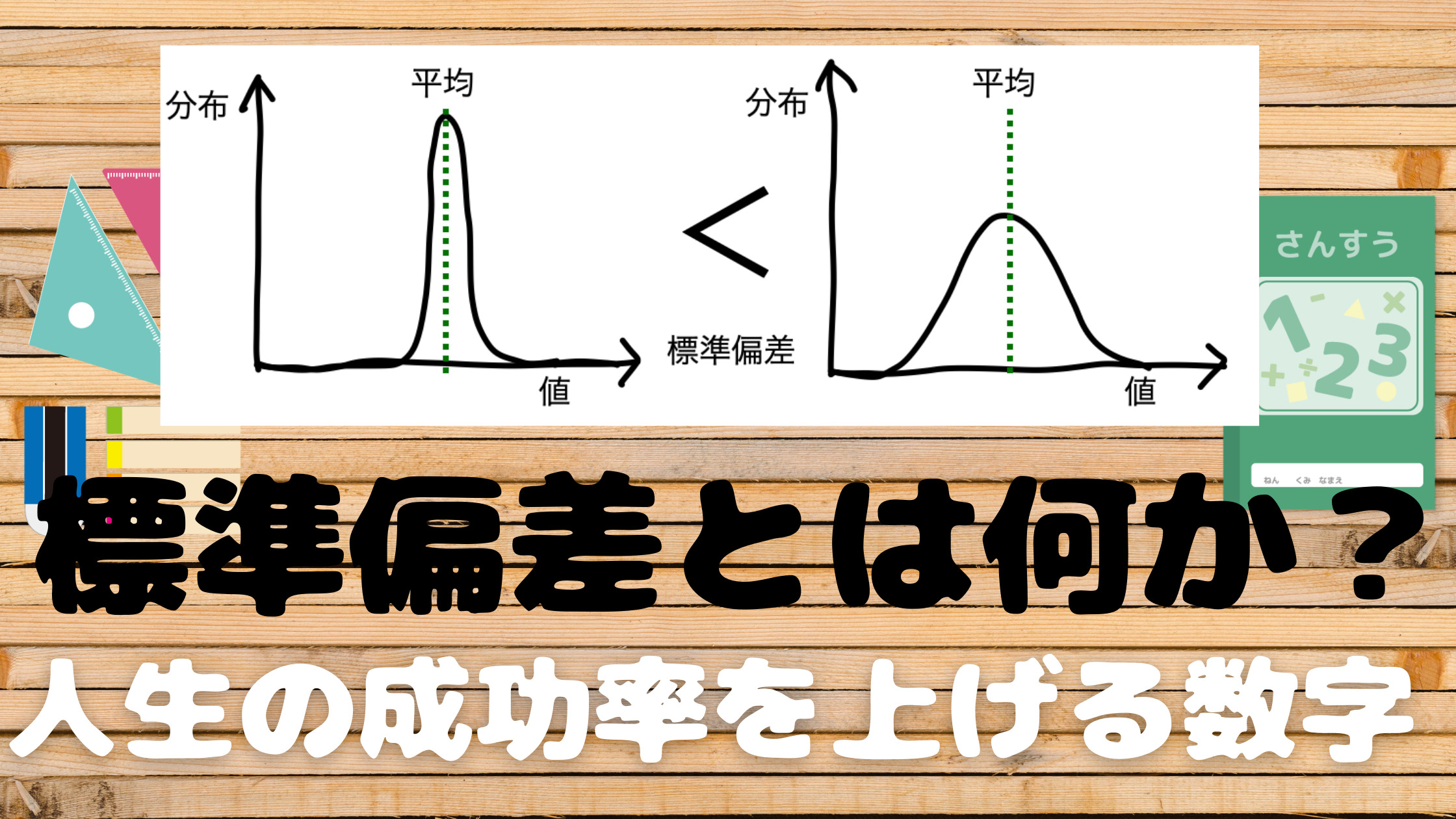
標準偏差は前述の正規分布における「データ(誤差)のバラツキ具合」を表しています。つまり、先ほどのグラフで表すと、
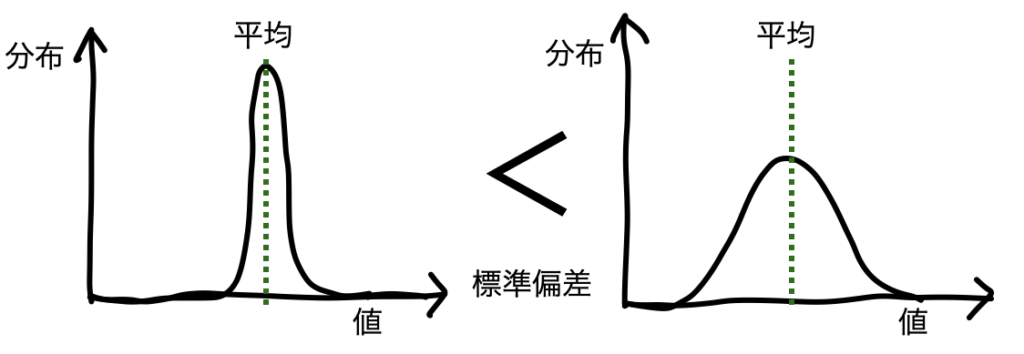
となります。

平均と離れるケースが多い、という場合は標準偏差が大きくなるんだね。
確率的な話をすると、以下のようになります。
- 平均値からの誤差が標準偏差の範囲内である確率は68.27%
- 平均値からの誤差が標準偏差の2倍の範囲内である確率は95.45%
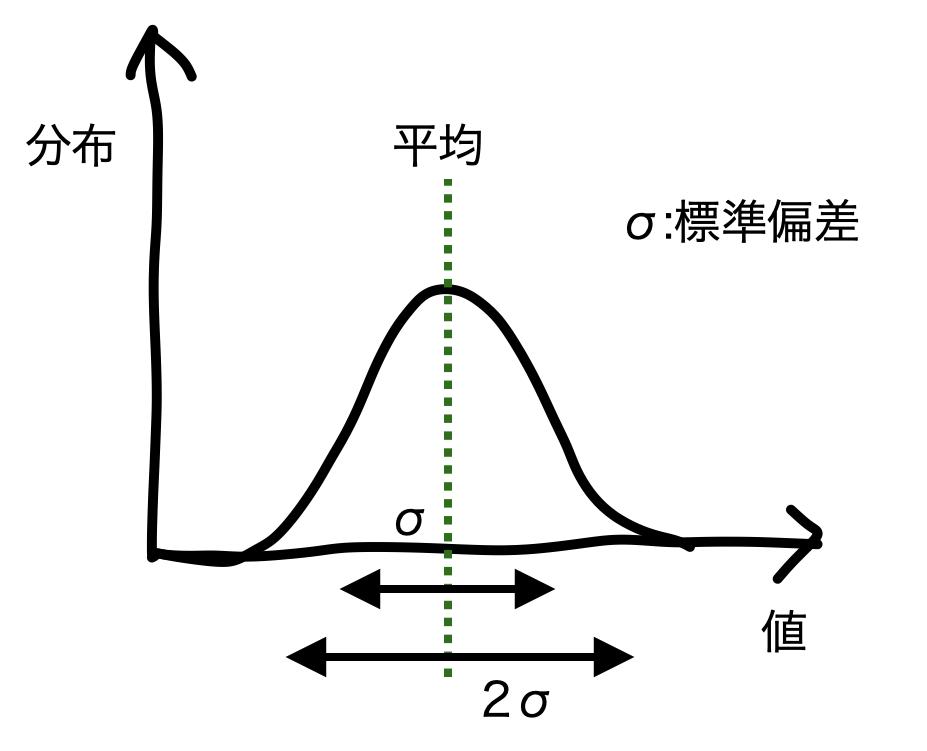

言い方を変えると、不確実な事象を確実っぽい事象(発生確率が高い)として扱うためには標準偏差が大きければ大きい事象ほど、大きな誤差を許容しないといけない訳です。
不確実な現象って嫌じゃないですか、なるべく確実な現象にしたいんです。そのために許容すべき誤差だと思っても過言ではありません。
言い方を変えると、標準偏差が大きい=想定外なことが起きやすいとも言えます。
- 誤差が大きくなりやすい
- 想定外のことが起きやすい
- 極端に大きい・小さい場合がありえる
- 結果のバラツキが大きい
- 平均をとるのが難しい

実は上記は全部同じことを言っていますが、日常生活のあらゆるところで言葉を変えて標準偏差は登場します。
人生の攻略法が分かる!標準偏差が使われる例
ここからは具体的に標準偏差を知ることで何が分かるのかを挙げることにします。
受験における力の入れ方が分かる
以下は令和2年の大学入試センター試験の地理歴史のデータです。
| 教科 | 平均点 | 標準偏差 |
|---|---|---|
| 世界史B | 62.97 | 22.46 |
| 日本史B | 65.45 | 19.43 |
| 地理B | 66.35 | 14.74 |
これを見て、どう思うかですが、まず気になるのは平均点ですね。

世界史Bが平均点が低い。不利だ!
いやいや、それはそうなのかもしれませんが、標準偏差でみると世界史Bが一番大きいですよね。つまりこういうことです。

世界史Bは平均点からのバラツキ(誤差)が大きい、つまり「できる人はめっちゃ点数取って、できない人は悲惨な点数を取った」ということです。
すなわち、標準偏差の大きな教科を得意教科にすると有利ということなんです。
地理歴史はこれまでも日本史/世界史の標準偏差が地理に比べて高い傾向にあります。
大学入試センター試験(今後は大学入学共通テスト)は受験者数が多いため、極端に標準偏差が大きくなるように出題されることは考えにくいです。
しかし、各大学での試験において標準偏差が公表しているのであれば絶対チェックすべきです。(有名大学であればその大学向け模試のデータでもよい)
標準偏差が大きな教科を苦手にしていると不利ですし、逆に標準偏差が小さな教科はすごい頑張っても平均点を大幅に超える点数が出せないので、力の入れ具合が違ってきます。
- 標準偏差が大きな教科が得意教科だと有利!
- 標準偏差が小さな教科に力を入れすぎると非効率!

ただし、だれぱんが言っているように、平均点の低い教科は標準偏差に差がなければ不利なことには変わりがないため、平均点ももちろんチェックする必要があります。
資産運用におけるリスクがわかる
資産運用において、よく出てくる言葉が「リスク」です。
株式投資などの資産運用の世界で、リスクについて議論されることが多いのですが、時々「リスク」という言葉の認識違いでミスコミュニケーションが起きているところに遭遇します。
「リスク」を辞書で調べると、以下になります。
危険の生じる可能性。危険度。また、結果を予測できる度合い。予想通りにいかない可能性。
デジタル大辞泉(小学館)より
上記から「リスク」の意味について、自分には2通りの意味の解釈があると思っています。
- 失敗する可能性(成功or失敗のゼロイチ世界)
- 結果が想定より大きく異なる可能性(バラツキ度合い)
使用例として、「リスク資産」といえば①の解釈に近く、「リスク分散」といえば②の解釈に近いように感じます。

繰り返しになりますが、あくまで自分の解釈です。
ただ、②の場合は想定より大きく結果が良かった!大成功!というケースもあるので、その上では①と②は同じ「リスク」という言葉の違う解釈と言えます。
「標準偏差とは何か?」の説明から考えると、標準偏差は②の解釈を持つ「リスク」を指しています。
すごく簡単にいうと、標準偏差が大きいものがハイリスク・ハイリターンで、標準偏差が小さいものがローリスク・ローリターンです。
試しに、eMaxisSlimシリーズの過去1年の平均リターン及び標準偏差をみんかぶ投信から見てみましょう。
| 銘柄 | 過去1年平均リターン | 過去1年標準偏差 |
|---|---|---|
| eMAXIS Slim米国株式(S&P500) | 5.96% | 20.66 |
| eMAXIS Slimバランス(8資産均等型) | -1.70% | 15.11 |
| eMAXIS Slim先進国債券インデックス | 6.15% | 3.00 |
平均だけ見ると、

先進国債権の利回りすごくね!
となるのですが、標準偏差を見ると状況が変わります。
先進国債権は確かに平均リターンは高いのですが、標準偏差が小さいためここから大幅に上下することはあまりないです。
一方で残りの2つは標準偏差が高いため、ここから大幅に上下する可能性があります。
この上下する幅をボラティリティとも呼び、リスクの大きさを表しています。
ボラティリティを意識して自分のリスク許容度にあった資産に投資しないと、過大な損失を受ける可能性があります。
- 標準偏差が大きな資産はハイリスク・ハイリターン!
- 標準偏差が小さな資産はローリスク・ローリターン!

では何で8資産均等(株式、債権、リートが混ざったファンド)の平均リターンがマイナスになったのでしょうか?
もう1つデータを出します。こちらは6ヶ月のデータしかなかったのであえて上には載せませんでした。
| 銘柄 | 過去6ヶ月平均リターン | 過去6ヶ月標準偏差 |
|---|---|---|
| eMAXIS Slim先進国リートインデックス | -21.64% | 35.72 |
標準偏差の大きなリート(不動産)がマイナスの誤差を生み、足をひっぱりまくっていました・・・
そのマイナスを株式・債権がそれをカバーできなかったと考えられます。
見積もり精度の向上に使用できる
ソフトウエア開発のプロジェクトマネージメントにおいて見積もり手法は様々あります。
例えば、機能A〜Cの開発を実施する見積もりを行う場合、過去に同様の開発を実施した場合の実績値が以下だったとしたら、どう見積もるのが適切でしょう。
| 機能名 | 平均工数[人月] | 標準偏差 |
|---|---|---|
| 機能A | 1.0 | 0.2 |
| 機能B | 3.0 | 0.2 |
| 機能C | 3.0 | 1.0 |
標準偏差が小さい機能Aと機能Bは「ほぼほぼ平均工数で開発可能」なのに対して標準偏差が大きい機能Cは「いろいろトラブルが起きやすく、3.0人月を大幅にオーバーすることもある」と読み取れます
したがって、標準偏差が大きい機能Cは多めの見積もりが必要になります。
以下の確率で考えるのであれば、機能Cが2.0人月〜4.0人月で開発できる可能性は68.27%で、1.0人月〜5.0人月で開発できる可能性は95.45%になります。
- 平均値からの誤差が標準偏差の範囲内である確率は68.27%
- 平均値からの誤差が標準偏差の2倍の範囲内である確率は95.45%

- 標準偏差が大きな作業は多めに見積もる(バッファを多めに積む)
- 標準偏差が小さな作業はこれまでの実績値で見積もる(バッファをあまり積まない)
まとめ:標準偏差は平均とセットで考えると人生の作戦が立てられる
これまで挙げた「入学試験」「資産運用」「見積もり」は今まで自分が経験した標準偏差が登場したパターンです。
- 標準偏差が大きな教科が得意教科だと有利!
- 標準偏差が小さな教科に力を入れすぎると非効率!
- 標準偏差が大きな資産はハイリスク・ハイリターン!
- 標準偏差が小さな資産はローリスク・ローリターン!
- 標準偏差が大きな作業は多めに見積もる(バッファを多めに積む)
- 標準偏差が小さな作業はこれまでの実績値で見積もる(バッファをあまり積まない)
一般に、起きることが100%である事象は、対策すれば効果があります。
今回は取り挙げた事象は起きることが100%ではない不確実事象です。
不確実な事象であっても、起きる想定を100%になるべく近づくようにして、対策の効果を最大限に発揮するために標準偏差を使いました。
なかなか世の中は上手くいかないことが多いですが、何も考えずにただ祈るよりも、平均と標準偏差をセット考えて作戦を立てる方が勝率が上がる前向きな対応ではないかと思います。

過去の先人の知恵を味方につけて、人生の勝率を上げていきましょう!
今回は標準偏差にフォーカスを当てましたが、その前提は「平均」を使いこなすことなので、平均も忘れずに。

標準偏差は小さくて「確実に資産形成できる」と言われても、平均リターンがマイナスならばほぼ確実に負けますからね。(手数料や信託報酬バカ高の資産ならばありえる)